- PDF:PDF版をダウンロード
- DOI: http://doi.org/10.15108/stih.00112
- 公開日: 2018.02.26
- 著者: 奥山 知香子、科学技術予測センター
- 雑誌情報: STI Horizon, Vol.4, No.1
- 発行者: 文部科学省科学技術・学術政策研究所 (NISTEP)
ナイスステップな研究者から見た変化の新潮流
京都大学大学院 情報学研究科通信情報システム専攻
François Le Gall 特定准教授インタビュー
-量子計算の考え方を用いて世界最速の“行列のかけ算”を実現-
科学技術予測センター
昨今、AI(人工知能)やビッグデータという言葉が一般にも用いられるようになった。第5期科学技術基本計画でもSociety5.0など、情報技術を高度に活用する社会の像が描かれており、こうした技術は様々な「計算」により支えられている。この「計算」についての最先端である「量子計算」の知見を活用し、古典的ながら重要な“行列のかけ算”(行列積)の世界最速アルゴリズムを開発した研究者が、ナイスステップな研究者2017に選定された京都大学大学院のFrançois Le Gall(フランソワ・ルガル)特定准教授である。今回はLe Gall特定准教授に量子計算や行列積、そして先生の御出身であるフランスの教育制度などについてお話を伺った。

京都大学大学院 特定准教授
― Le Gall先生の研究内容について御紹介をお願いします。
大きく言うと情報科学分野でアルゴリズム、いわゆる「計算の仕方」についての研究を行っています。どういう計算をコンピュータに任せられるか、また、どのようにすれば計算を高速化、効率化できるか、といったことに取り組む分野です。
私自身はその中でも「量子計算」を扱っています。量子計算は「量子コンピュータ」という、皆さんがふだん使っているコンピュータとは性質(計算の方法)が大きく異なるコンピュータ上で、どういう計算をさせられるか、といったこと等を考えるものです。
最近では一般のニュースでも「量子コンピュータ」という言葉が出てくることがあるので、どこかで「量子コンピュータ」という単語を耳にしたことがあるとか、さらに、何となくどういうものか御存じの方も多いかもしれません。「量子コンピュータ」は量子力学の原理を用いて計算をするもので、これは、皆さんもふだん使っているこれまでのコンピュータとは全く異なる発想のものになります。結果として、これまでのコンピュータと比較してとても高速な計算が実現でき、現在主流になっている暗号をあっという間に解読するようなこともできるようになる、と言われています。
ただ、「量子コンピュータ」にはいろいろ制約もあって、どんな種類の計算でもできるというわけではないのです。では、どういう種類の計算ならできるのか。あるいは、どの計算はできないのか。それを明らかにしようというのが「量子計算」のテーマの一つです。
「量子計算」の面白さは、その原理的な部分にもありますが、取り組む人材、コミュニティの面にも面白さがあります。例えば、量子力学は主に物理学で議論がされているものですし、更に数学や情報科学などの知識も必要になります。そのため、研究コミュニティ内における研究者のバックグラウンドが非常に多様です。そして、このように多様な人々が、同一の目的・目標に対して一緒に取り組んでいる、という面にも面白さがあります。
― Le Gall先生は「量子計算」の他、「行列積」というテーマについても優れた成果をお持ちです。「行列積」について、御紹介をお願いします。
今回、科学技術・学術政策研究所(NISTEP)から「ナイスステップな研究者2017」として選定されたのも、「行列積」の高速化に関する成果を評価いただいたからだと伺いました。大変光栄です。ありがとうございます。
「行列積」そのものは「量子計算」とは別種のもので、2010年か2011年頃から取り組み始めたものですが、2014年に世界最速となる計算手法を開発することができ、国際会議で賞をいただくこともできました。
「行列積」は名前のとおり行列同士のかけ算、行列の積です。とても基礎的なもので、実際の操作も、かけ算と足し算を繰り返すだけの単純なものです。
日常生活の中で、皆さんが直接、行列積を扱うようなことはないかもしれませんが、様々な物理現象の計算には必須の演算で、足し算と同じくらいの感覚で、多くの場面で用いられています。例えば、IoTなどのセンサデータを処理するとき、画像を処理するとき、人工知能を用いて何かのデータを解析するときなど、挙げればきりがありません。
― 「行列積」の高速化とはどのようなものですか。
計算の高速化といっても様々なアプローチがあります。詳しい方は、複数のコンピュータを使って計算を分散・並列処理をする、というような手法にはなじみがあるかもしれません。一方、私は“計算の回数を減らす”ことで高速化を図りました。2017年12月20日現在において、私が提案した計算手法を使うと最も少ない計算回数で、行列積の答えを求められるということですね。
一番単純に(正方行列同士の)行列積の答えを得ようとすると、行列のサイズに応じて、その3乗回ほど計算をしなければなりません。行列のサイズをnとしたとき、3乗回ほど計算をすることをO(n3)と表現します。私の手法ではこの計算時間の指数をO(n2.3728639)まで圧縮することができました。計算の回数が少ないほど早く計算を終えることができるので、この計算回数の削減はとても大事です。特に最近はハードウェアが整って高速に計算できるようになったり、大量のデータを蓄積しやすくなったりしています。その結果、nのサイズが数万だったり、それ以上だったり、という行列を扱うこともそんなに珍しいことではなくなってきました。また、行列自体はそんなに大きくなくとも、行列積を膨大な回数実施することがあります。そうすると、ごくわずかな計算量の削減でも、あっという間に数百、数千、数万時間という時間削減ができる。その時間の差が勝敗を分けたり、未来を大きく変えたりすることも大いにあり得ます。
今でもコンピュータが日常空間の至る所にありふれていて、様々なデータが収集・分析されていますが、こうした傾向は今後も続いていくと思います。情報技術を活用したより良い未来のために、計算量の削減はますます重要になると思います。
― 「行列積」の高速化はLe Gall先生が初めて思いつかれたものですか。
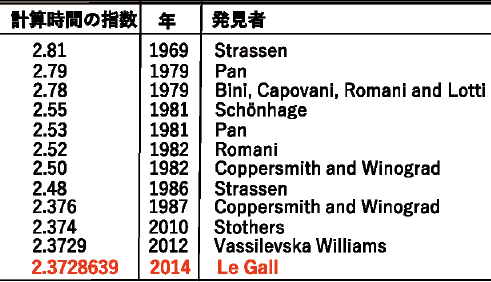
先ほど申し上げたとおり、「行列積」は基礎的な演算です。そのため、これを高速化しよう、計算量を削減しようという取組は古くから行われていました。こちらの表(図表1)に行列積の計算量削減の歴史をまとめてみました。
もともと行列積の計算量はO(n3)なのですが、1969年にこれを削減する方法(Strassen法)が提案されました。行列積の計算量を削減できることが明らかになったという点で、これはとても衝撃的な成果であり、ここから行列積の計算量削減に注目が集まったと思います。ただ、その後の成果はなかなか出ず、次に削減されたのはその10年後の1979年です。そこから1980年代まで、少しずつ改良が進みました。
その後はかなり間が開いて、2010年になってようやく進展しています。私が行列積に取り組み始めたのもこの頃ですね。時期的には、2010年のStothers、2012年のVassilevska-Williams、2014年の私と近いのですが、3チームともほぼ独立に研究を進めて改良をしています。
2010年代に急に成果が出ているのは、昨今のAIブームと似た部分があって、コンピュータの性能が上がり、大量・高速な計算が可能になったことが挙げられると思います。私の場合はさらに、従来の行列積の計算量削減の方式に、量子計算で培った知見を導入したことで、良い成果を出せたと思います。

― このテーマに取り組んだきっかけ、行列積の面白さ、今後の研究の方向性などについて、お聞かせください。
取り組んだきっかけですが、そもそも量子コンピュータ上で行列積を高速に行えないか、という疑問を追及したことが始まりです。結局そのとき得られたのは小さな成果だけだったのですが、行列積自体は面白いテーマと感じましたので、普通のコンピュータ上での高速化、すなわち計算量削減ができないか考えよう、ということで取組を始めました。
行列積は、非常に単純なものなのに、計算量がどこまで減らせるかといったこともわかっていない、というのが面白いですね。問題設定はとてもわかりやすいのに、答えを出すのはとても難しい、という意味では、フェルマーの最終定理やABC予想などと通じるところがあるかもしれません。
今申し上げたとおり、行列積の計算量がどこまで減らせるかはいまだ明らかになってはいません。そのため、根拠となるものはないのですが、研究者の間では感覚としてO(n2)まで削減できるのではないか、と言われています。私もまだ削減できると思っているので引き続き取り組んでいきたいテーマの一つです。また、私自身では取り組みづらいところとして、提案した計算手法が様々なプログラミング言語で実装され、手軽に利用されるようになればうれしいと感じています。
また、今回は量子計算の考え方を使って行列積の計算を高速化しましたが、同様に量子計算の考え方を、(量子計算ではない)一般的な計算に生かせる事例があると考えています。そこで、量子を利用した計算と一般的な従来のコンピュータの計算の関係性を究明することで、より計算能力を上げるような研究をしていきたいと思います。
― ここから少し全体的なお話を伺いたいと思います。量子計算や行列積など情報科学系のテーマに興味を持ったのは、いつ頃ですか。
小学生のときから数学とコンピュータは好きで、その頃からプログラミングなども行っていました。その意味では、情報科学分野の選択は自然なことでした。
ただ、始めから量子計算などに取り組んでいたわけではなく、日本に来てすぐ、東京大学で修士課程に在籍していた頃はニューラルネットワークの研究をしていました。ニューラルネットワークは現在はやっているディープラーニング(深層学習)の基本となる技術です。ただ、そこでは思うほどの成果が出ず、博士課程では別のことをしてみようといろいろ検討しました。その際に、当時ホットな分野だった量子計算を選んで今日に至っています。冒頭でもお話ししたとおり、量子計算の分野は様々なバックグラウンドを持つ人が研究に取り組んでいるため、国際学会などに行くと非常に刺激を受けます。「(計算を利用して)見た目では違う分野をつなげてみたい」というのも、量子計算を選んだ理由の一つです。
― 今お話を頂いたとおり、Le Gall先生は東京大学で修士・博士課程を修了されています。留学先に日本を選んだきっかけはどのようなものでしたか。
留学先は幾つかの候補を検討はしていました。ただ、もともと漢字など東洋の文化にも興味があり、大学時代に日本語の授業もとっていたこと、当時の文部省が留学生向けの奨学金制度を提供してくれていたこと、などから日本への留学を決めました。
当時は数年留学して帰国し、企業に就職しようかな、と考えていたので、まさかこんなに研究が楽しくなって、様々な御縁もできて、16年も日本で過ごすことになるとは想像していませんでした。
― Le Gall先生はフランス御出身ですが、フランスと日本の教育・研究制度については様々な違いがありそうです。例えば、フランスでは高校から哲学の授業が必須であるという話もよく耳にします。両国で過ごす中で何か気づいた点があれば教えてください。
研究活動は日本でしか行っていないので、比較することは難しいです。そこで、飽くまで個人的な体験、一事例としてお答えさせていただきます。
教育については御指摘のとおり、母国のフランスでは高校から哲学の授業をしっかりやります。日本のセンター試験に相当するバカロレアでも哲学の試験があります。バカロレア自体はセンター試験に比べれば簡単なものですが、選択式の問題は一切なく記述式である点が面白いところでしょうか。哲学の問題であれば「科学は人類に幸せをもたらすか」みたいな短いテーマが一つ与えられて、その回答を4時間かけて作文します。こうした問題は物事の見方、思考力を鍛える、という意味で良かったと思います。
大学については、留学後に「研究室」の存在や、修士課程でしっかり研究をする点に驚きました。現所属の京都大学では数学科などは「研究室」という単位では活動をしていないようですが、フランスでは他の学部もそうした感じです。学生にも個人個人でやりたい、明らかにしたいことがあって、必要に応じて、関連する先生に話を聞きに行く、そういうスタイルがフランスでは一般的ということですね。
日本では研究室単位で行動して、食事も仕事もその単位で動くので新鮮でした。もちろん、これらはどちらが良い・悪いというものではありません。私は留学生で日本のことは右も左もわかりませんでしたので、この研究室という制度は生活の面でもとても助かりました。研究面でも、テーマ選定から系統的にサポートを得られる点で助かりました。
修士課程の学生の生活については、フランスでは、少し高度な授業を受けるのとインターン、最後に比較的短期間で実施できる研究を行う、というケースが多いように思います。研究に打ち込む期間が短い代わりに、インターンは在学中に1回数か月のものを最低2回、そのうち1回は海外を必須、とするケースをよく見聞きしました。その意味でもインターンの比重は日本と比較するととても大きいと思います。インターンを通じて、学生と企業の双方のニーズ・シーズをすりあわせるためか、就職後ももともとの専門を生かした職種に就く学生が多い印象ですね。博士課程の学生が研究をしっかり行う点はフランスでも日本でも同じと思います。
― 最後に、学生に向けてのメッセージをお聞かせください。
何か一つ興味、関心を持てるテーマを見つけて、それをしっかり突き詰めてみる、ということがとても大切だと思っています。自分なりの哲学をしっかり築く、と言い換えられるかもしれません。
教師の側としては、その興味、関心を最大限引き出せるよう努力しています。例えば、数学の授業でも古典的な理論を教授するだけでなく、最先端の理論や成果を紹介するように心がけています。そうすることで、学問も生き物で日々変化していることや、生活と結びついていることを実感してもらうことができるのではないか、興味、関心を呼び起こせるのではないかと期待しています。
ちなみに量子計算はこれからますます重要な分野になってくると思います。修士課程では時間が足りないかもしれませんが、博士課程では面白いテーマをいろいろと見つけられると思います。


